Big O notation in 2 mins

Time complexity measurements

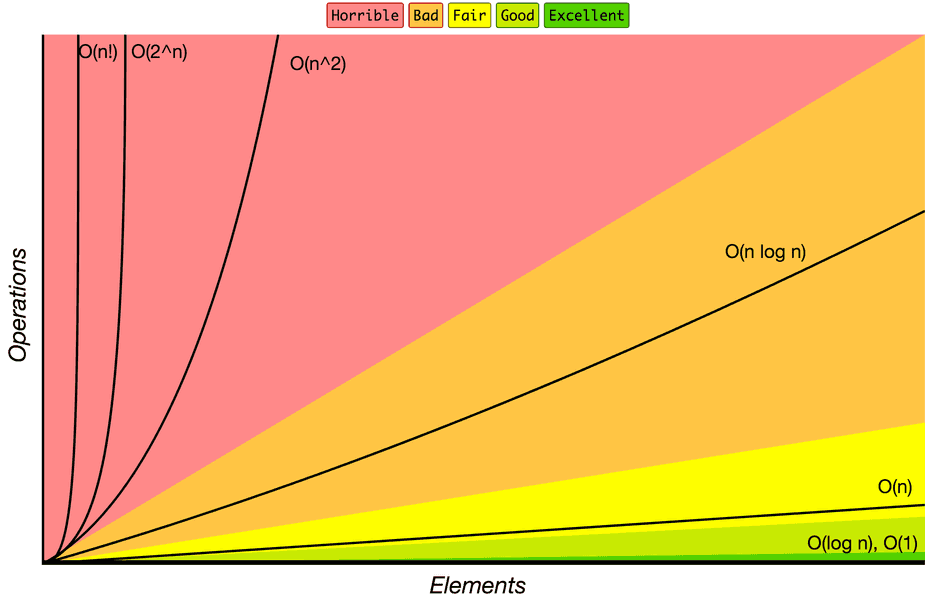
Big O notation is a relatively simple way for people to discuss the expected growth in time to run and auxillary space of an algorithm. It helps us answer the question “Will it scale?” and helps to compare algorithm solutions to see which is best.

Measuring time complexity

0(1) - constant complexity

    function print(x) {  
        console.log(x);  
    }

An algorithm that will take the same amount of time regardless of the size of the inputs. If x is 1 item or 1000 items this function time to complete will not grow.

0(log n) - logarithmic

while (x > 0) {  
   x /= 2;  
   console.log(x);
}  

An algorithm O(log n) is usually when they divide and conquer, such as binary search or similar.

0(n) - linear

    function printEach(arrayOfThings) {  
        arrayOfThings.forEach( x => {
            console.log(x);  
		});        
    }

An algorithm that will take will grow at a linear rate. If you input 10 items, it has to print 10 items. For 10,000 items it has to print it 10,000 times.

0(n^2) - Quadratic

    function printAllPairs(n) {  
        for(let i = 0; i < n; i++) {
            for(let j = 0; j < n; j++) {
	            console.log(i,j);
            }
        }        
    }  

An algorithm that will scale at the rate of n squared.

0(2^n) - Exponential

int fibonacci(int num)
{
    if (num <= 1) return num;
    return fibonacci(num - 2) + fibonacci(num - 1);
}

An algorithm whose growth doubles with each addition to the input data set. The growth curve of an O(2^n) function is exponential - starting off very shallow, then rising quickly.

0(n!) Factorial

    function printAllNumbers(num) {  
        for(let i = 0; i < num; i++) {
            console.log(num); 
            printAllNumbers(num-1);           
        }        
    }